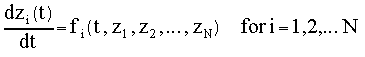Introduction
Inheritance
  Demo 1
Overriding
  Demo 2a   Demo 2b
this,super
MoreConstructors
  Demo 3
Abstraction
Interface 
  Demo 4
Casting References
MoreAboutArrays
Object class
Class Summary
Exercises

For the shooting method (ref) we consider a set of N differential equations

for N variables. We set n initial conditions at t₁ :

This means n of the variables will have fixed initial values. This in turn means that m = N-n of the variables have unspecified inital values. We will call these the free variables.

If we have m = N-n final conditions at t₂ :

then the goal is to vary the initial values of the m free variables until we get the variables to match the boundary conditions at t₂.

For each set of these initial values, we integrate the variables from t₁ to t₂. (This is the shooting step.) The difference between the final values and the desired boundary values is set up as a function to be minimized by a root-finding method, such as discrete Newton method.

The process begins by setting the n variables to their fixed values and guessing at values for the m free variables. Lets label these initial values for the free variables as

We then use an ODE method such as Euler or Runge-Kutta to integrate the variables over the interval t₁ to t₂.

The boundary conditions demand that m of the variables match specific values at t2 :

      for m of the variables

We create a function proportional to the total distance of the final values from the boundary values as in

The root-finding method varys the Z₁(t₁),..Z_m(t₁) values until F equals zero.

In summary, the algorithm makes a guess at the initial values of the free variables and integrates over t₁ to t₂ interval, that is, it shoots towards the target. Based on the distance of the values from the target values, the algorithm modifies the initial values of the independent variables and tries the integration again. This interative procedure eventually results in a close hit on the final value. If the differential equations are linear, then this method will require only one iteration.

Another technique is to shoot from both the initial and and final boundaries and try to meet at an intermediate point (see ref). Here we look only at the first technique as discussed in Demo 3.

            Tech
MoreComplexClass
ImprovedHistogram
JavaRandomNums
Vectors & Matrices
Exercises

           Physics
Runge-Kutta 2nd
  Demo 1
Runge-Kutta 4th
  Demo 2
BoundaryVal.Prob
Shooting Method
  Demo 3
Exercises