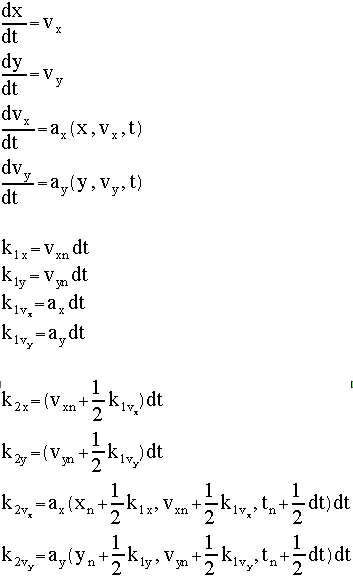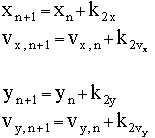Home : Map : Chapter 4 : Java : Tech : Physics :
Demo 1: Projectile Motion with 2nd Order R-K
JavaTech
Course Map
Chapter 4

Introduction
Inheritance
  Demo 1
Overriding
  Demo 2a   Demo 2b
this,super
MoreConstructors
  Demo 3
Abstraction
Interface 
  Demo 4
Casting References
 MoreAboutArrays
Object class
Class Summary
Exercises

    Supplements
Override/Overload
Annotation-J2SE5.0
Java Security
Class Loading
Class Verifier
SecurityManager
     About JavaTech
     Codes List
     Exercises
     Feedback
     References
     Resources
     Tips
     Topic Index
     Course Guide
     What's New

The 2nd Order Runge-Kutta formula shown above is for a single variable x, which would suffice for determining the motion of a falling object or for an object on spring. For projectile motion, though, we deal with two coordinates.

We thus need formulas for both vertical (y) and horizontal (x) variables:

        

and then

    

Below we show the code for a second order Runge-Kutta class that generalizes the above formulas to multiple variables. Array arguments carry the variables and their derivative. Here we use the name vel, as in velocity, for the derivatives but these could be derivatives with respect to a non-time related variable.

The derivative of the velocity comes from an interface method called Derivable, shown below. The method modifier static eliminates the need to create an instance of the class.

RungeKutta2nd.java
/** Carry out the Runge-Kutta 2nd order algorithm. **/
public class RungeKutta2nd
{
  /** Calculate as step in the Runge-Kutta 2nd order. **/
  public static void step (double t, double dt,
                    double [] var,
                    double [] vel,
                    Derivable func )  {

     double k1_var, k1_vel;
     double k2_var, k2_vel;

     for (int i=0; i < var.length; i++) {
       k1_var = vel[i] * dt;
       k1_vel = func.deriv (i,var[i],vel[i],t)*dt;

       k2_var =  (vel[i] + 0.5*k1_vel)*dt;
       k2_vel = func.deriv (i,
                            var[i] + 0.5*k1_var,
                            vel[i] + 0.5 * k1_vel,
                            t+0.5 * dt) * dt;

       var[i] = var[i] + k2_var;
       vel[i] = vel[i] + k2_vel;
    }

    t += dt;
  } // step

} // RungeKutta2nd
Derivable.java

public interface Derivable
{
   public double deriv (int i, double pos, double v,
                              double t, double t);
} // Derivable

 

The program below uses the second order Runge-Kutta code above to solve for the intercept of a projectile with the horizontal plane. Ignoring air drag (see the exercises), the horizontal force is zero and the vertical force is a constant.

Note how the class implements the interface and overrides its method.

RK2ndApplet.java
(Output goes to browser's Java console.)
/**
  * This applet uses the second order Runge-Kutta method
  * to solve for the landing point of a projectile.
 **/
public class RK2ndApplet extends java.applet.Applet
  implements Derivable
{
  // Constants
  double g  = 9.80;// meter per sec**2
  double x0 = 0.0;
  double y0 = 0.0;
  double v0 = 100.0;// initial vel, m/s
  double angle = Math.PI/4.0;

  // Instance variables
  double [] pos = new double[2];
  double [] vel = new double[2];

  /** Initialize the algorithm. **/
  public void init () {

    double t;
    double total_t;
    int n;

    double dt =  0.01;
    int n_steps = 100000;

    pos[0] = x0;
    pos[1] = y0;
    vel[0] = v0 * Math.cos (angle);
    vel[1] = v0 * Math.sin (angle);
    t = 0.0;

    for (n=0; n < n_steps; n++) {
      RungeKutta2nd.step (t,dt,pos,vel,this);
      if (pos[1] <= 0.0) break;
    }
    System.out.println ("After steps =" + n);
    System.out.println (" x = " + pos[0]);

  } // init

  /** Implement the interfact method for the derivative
    * of the variables. **/
  public double deriv (int i, double newVar, double newVel, double t) {
    if (i == 0) {// x variable
      return 0.0;
    } else { // y variable
      return -g;
    }

  } // deriv

  /** Paint message in Applet window. **/
  public void paint (java.awt.Graphics g) {
     g.drawString ("RK2ndApplet",20,20);
  } // pain

  /** Run optionally as an application. **/
  public static void main (String [] args) {
    RK2ndApplet obj = new RK2ndApplet ();
    obj.init ();
  } // main

} // RK2ndApplet

 

The output shows

After steps =1443
   x = 1021.0621920333822

 

This compares to a value of 1020.4 for the analytical solution.

Exercise : Try a finer dt value to see if the intercept makes a better match to the analytical value.

Exercise : The program checks if the projectile vertical coordinate has become negative to indicate that the object has reached the surface. However, this can overestimate the horizontal intercept. Add code to do an interpolation to obtain a more accurate intercept.

 

Most recent update: Oct. 21, 2005

            Tech
MoreComplexClass
ImprovedHistogram
JavaRandomNums
Vectors & Matrices
Exercises

           Physics
 Runge-Kutta 2nd
  Demo 1
Runge-Kutta 4th
  Demo 2
BoundaryVal.Prob
Shooting Method
  Demo 3
Exercises

  Part I Part II Part III
Java Core 1  2  3  4  5  6  7  8  9  10  11  12 13 14 15 16 17
18 19 20 21 		22 23 24
Supplements

1  2  3  4  5  6  7  8  9  10  11  12
Tech 1  2  3  4  5  6  7  8  9  10  11  12
Physics 1  2  3  4  5  6  7  8  9  10  11  12

Java is a trademark of Sun Microsystems, Inc.