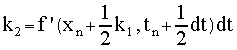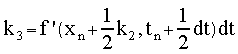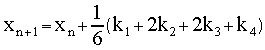|
A further refinement of the Runge-Kutta approach uses
derivatives at the beginning of the interval, at the end of the
interval and twice at the midpoint.
Using the conventional k#
variable names, we obtain the following increments in the variable
xn
with :
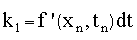
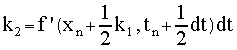
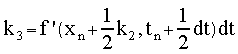
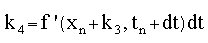
Then the new increment in variable x
is calculated as a weighted average of these estimated increments
with k2
and k3
, the two midpoint values, given double weights.
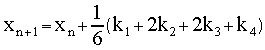
The code below shows a class created to carry out the 4th order
Runge-Kutta algorithm.
| RungeKutta4th.java
|
|
/**
* Provides a static method to calculate the
4th order
* Runge-Kutta integration calculation.
**/
public class RungeKutta4th
{
/**
* Calculated a step of the integration
of an ODE with
* 4th order RK.
*
* @param t independent
variable
* @param dt step in the independent
variable
* @param var array holding the dependent
variable
* @param vel array holding the first
derivative
*
**/
public static void step (double t, double dt,
double [] var,
double [] vel,
Derivable func ) {
double k1_var, k1_vel;
double k2_var, k2_vel;
double k3_var, k3_vel;
double k4_var, k4_vel;
for (int i=0; i < var.length; i++)
{
k1_var = vel[i] * dt;
k1_vel = func.deriv
(i,var[i],vel[i],t)*dt;
k2_var = (vel[i]
+ 0.5*k1_vel)*dt;
k2_vel = func.deriv
(i,var[i] + 0.5*k1_var,
vel[i] + 0.5*k1_vel,
t+0.5*dt)*dt;
k3_var = (vel[i]
+ 0.5*k2_vel)*dt;
k3_vel = func.deriv
(i,var[i] + 0.5*k2_var,
vel[i] + 0.5*k2_vel,
t+0.5*dt)*dt;
k4_var = (vel[i]
+ k3_vel)*dt;
k4_vel = func.deriv
(i,var[i] + k3_var,
vel[i]
+ k3_vel,
t+dt)*dt;
var[i] = var[i] +
(k1_var + 2.0*k2_var
+ 2.0*k3_var + k4_var)/6.0;
vel[i] = vel[i] +
(k1_vel + 2.0*k2_vel
+ 2.0*k3_vel + k4_vel)/6.0;
}
t += dt;
} // step
} // RungeKutta4th
|
The example below is the same as previously except that the above
code for the 4th order Runge-Kutta is used to the step calculation.
RK4thApplet6.java
(Output goes to browser's Java
console.)
|
|
/** Program
using the second order Runge-Kutta method
* to solve for the landing point of a projectile.**/
public class RK4thApplet extends java.applet.Applet
implements Derivable
{
// Constants
double g = 9.80;// meter per sec**2
double x0 = 0.0;
double y0 = 0.0;
double v0 = 100.0;// initial vel, m/s
double angle = Math.PI/4.0;
// Instance variables
double [] pos = new double[2];
double [] vel = new double[2];
/** Set up for the algorithm. **/
public void init () {
double t;
double totalT;
int n;
double dt = 0.01;
int nSteps = 100000;
pos[0] = x0;
pos[1] = y0;
vel[0] = v0 * Math.cos (angle);
vel[1] = v0 * Math.sin (angle);
t = 0.0;
for ( n=0; n< nSteps; n++) {
RungeKutta4th.step (t,dt,pos,vel,this);
if (pos[1] <= 0.0) break;
}
System.out.println ("After steps
= " + n);
System.out.println (" x = " + pos[0]);
} // init
/** Implement the interface method for the derivative
* of the variables. **/
public double deriv (int i, double var, double
vel, double t) {
if (i == 0) { // x variable
return 0.0;
} else {// y variable
return -g;
}
} // deriv
/** Paint message in Applet window. **/
public void paint (java.awt.Graphics g) {
g.drawString ("RK4thApplet",20,20);
} // paint
/** Run optionally as a application. **/
public static void main (String [] args) {
RK4thApplet obj = new RK4thApplet
();
obj.init ();
} // main
} // RK4thApplet
|
The output shows
After steps
=1443
x = 1021.0621920333822 |
This is the same as for the previous example since
constant term for the acceleration results in the same increment
to x as with the 2nd order code.
Most recent update: Oct. 21, 2005
|