|
This demo applies the shooting
method to the actual task of literally shooting a projectile
at a target. The projectile begins from a given point and a given
horizontal velocity. The shooting method must determine the inital
vertical velocity component (vy_init)
that will send the projectile to hit the target vertical point after
traveling a 10 seconds.
A function (or score) is created using distance of
the target to the final vertical value of the projectile. The discrete
Newton (or secant) method is used to determine the root of this
function.
For each vy_init
point a 4th order Runge-Kutta integration of the trajectory is carried
out. The Newton method needs to calculate trajectory twice initially
and then once for each iteration.
For the projectile there are 4 (=N)
variables dependent on t
:
x(t)
- horizontal coordinate
y(t) - vertical coordinate
vx(t) - horizontal velocity
vy(t) - vertical velocity
Here we set three (=n)
variables to fixed initial values:
x(t1),y(t1)
- initial location
vx(t1) - initial horizontal
velocity
We guess at an initial value for the free variable
vy(t1)
One (=m)
of the four variables has fixed final values:
yb
- target point
The final velocities are not specified.
The program varies vy(t1)
such that the final y
values match the target point. The discrete Newton (secant) method
is used to find the root of
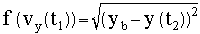
The following code shows the Shoot_Applet6.java code
that carries out the shooting algorithm. The helper class Shooter
below does the trajectory finding with the
4th order Runge-Kutta :
ShootApplet.java
(Output goes to browser's Java
console.)
|
/** Program using the shooting method to find the
initial
* vertical velocity component of a
projectile such that it
* hits a target point.
**/
public class ShootApplet extends java.applet.Applet
{
// Parameters for the algorithms
double dvy = 1.0;
double tol = 0.1;
double dt = 0.001;
int nSteps = 10000; // => 10 seconds of flight
int maxSteps = 2000;
double x_init = 0.0;
double y_init = 0.0;
double vx_init = 400.0;
double vy_init = 1.0;// first guess
// Set target point
double posTarget = 100.0;
// Create an instance of the shooting algorithm
class.
Shooter shooter = new Shooter ();
// These arrays hold the coordinates and velocities
// of the projectile at start and end.
double [] pos_final = new double [2];
double [] pos_init = new double [2];
double [] v_init = new
double [2];
double [] v_final = new
double [2];
/** Set up and then use the shooting method to
determine
* the initial velocities that led
to a projectile hitting
* the given target.
**/
public void init () {
// Set initial conditions.
pos_init[0] = x_init;
pos_init[1] = y_init;
v_init[0]
= vx_init;
v_init[1]
= vy_init;
// At step n, these variables hold
the
// nth, n-1, and n-2 values for the
velocity
// and scores.
double vyn, vyn_1, vyn_2;
double fn, fn_1, fn_2;
// Discrete Newton method needs 2
initial points.
vyn_2 = v_init[1]; // First guess
at vy_init
fn_2 = f ();
v_init[1] += dvy; // Second
guess at vy_init
vyn_1 = v_init[1];
fn_1 = f ();
int numSteps = 0;
do {
double divisor = (fn_1
- fn_2);
if (divisor == 0.0) {
System.out.println
("Derivative invalid");
return;
}
// Calculate new estimate
of the vy_init
// using the discrete
Newton (i.e. secant) method
double del = (vyn_1 -
vyn_2) * (fn_1)/divisor;
System.out.println
(" del = " + del);
vyn = vyn_1 - del;
v_init[1] = vyn; // new
vy inital estimate
// Calculate trajectory
with this new initial vy
// and return a "score"
for how close the shot came
// to the target.
fn = f ();
// Save the past two estimates
of the velocity
vyn_2 = vyn_1;
vyn_1 = vyn;
// Save past two score
values.
fn_2 = fn_1;
fn_1 = fn;
numSteps++;
} while (fn > tol && numSteps
< maxSteps);
System.out.println ();
System.out.println ("After steps =
"+numSteps);
System.out.println (" &
Newton steps = "+numSteps);
System.out.println ("Root vy_init
= "+v_init[1]+
" results in a distance = "+fn+
" from target");
}
/** Calculate the distance between the end point
of the
* trajectory of the projectile (as
calculated from the
* Runge-Kutta method) and the desired
target point.
**/
double f () {
// Shooter uses the Runge-Kutta method
to step
// the projectile through a trajectory
using
// the initial values passed here.
shooter.shoot (pos_init, v_init,
pos_final,v_final,
dt,
nSteps);
double val =
(posTarget-pos_final[1])*
(posTarget-pos_final[1]);
return Math.sqrt (val);
} // f
/** Paint message in Applet window. **/
public void paint (java.awt.Graphics g) {
g.drawString ("ShootApplet",20,20);
}
/** Run optionally as an application. **/
public static void main (String [] args) {
ShootApplet obj = new ShootApplet
();
obj.init ();
} // main
} // ShootApplet |
The Shooter class
implements the Derivable
class discussed earlier. The stopping point
for the integration comes when the horizontal position of the target
is passed. An interpolation back to the vertical plane at xb
is carried out to get a better estimate for the crossing
point.
| Shooter.java
|
|
/** Shoot
carries out a Runge-Kutta integration of a
* projectile trajectory.
**/
public class Shooter implements Derivable
{
// Constants
static double g = 9.80;// meter per
sec**2
// Instance variables
double [] pos = new double[2];
double [] vel = new double[2];
// Method to carry out trajectory calculation
void shoot (double [] pos_init,
double
[] v_init,
double
[] pos_final,
double
[] v_final,
double
dt, int nSteps) {
double t = 0.0;
int n;
pos[0] = pos_init[0]; // x
pos[1] = pos_init[1]; // y
vel[0] = v_init[0];
// vx
vel[1] = v_init[1];
// vy
for (n=0; n < nSteps; n++) {
RungeKutta4th.step (t,dt,pos,vel,this);
}
pos_final[0] = pos[0];
pos_final[1] = pos[1];
v_final[0] = vel[0];
v_final[1] = vel[1];
System.out.println (" In Shooter
after steps =" + n);
System.out.println (" x,y = " +
pos[0] + ", " + pos[1]);
} // shoot
/** Implement the interface method for the derivative
* of the variables. **/
public double deriv (int i, double var, double
vel, double t) {
if (i == 0) { // x variable
return 0.0;
} else { // y variable
return -g;
}
} // deriv
} // Shooter
|
For this case, only one interation of the Newton algorithm
is needed to find the root as this output shows:
In Shooter
after steps =10000
x,y = 4000.0000000006353, -479.99999999995055
In Shooter after steps =10000
x,y = 4000.0000000006353, -469.9999999999515
del = -57.00000000000099
In Shooter after steps =10000
x,y = 4000.0000000006353, 100.00000000006408
After steps = 1
& Newton steps = 1
Root vy_init = 59.00000000000099 results in a distance = 6.407674391084583E-11
from target |
Exercise: Try
some other values for the target, the starting values, the increment
sizes, etc to see that the program still finds the target and find
how quickly the method finds the solution.
Most recent update: Oct. 21, 2005
|
