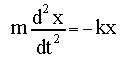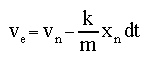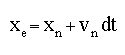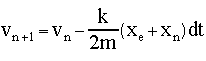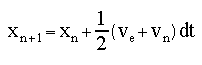Java Tech - Chapter 2 : Physics

For the this demonstration of the Euler method, we will look at the motion of a mass on spring:

The fallowing demo program compares the Predictor-Corrector values to analytical values.

Note: The program also illustrates several more Java language components such as the Math class functions and the modulo operator.

Spring_Applet1.java
(Output goes to browser's Java console.)

public class Spring_Applet1 extends java.applet.Applet
{
  public void init()
  {
    // Put code between this line
    //-----------------------------------------------
      int N = 100;
      int N_PRINT = 10;
      int N_CYCLES = 2;

      // One cycle per 100 steps
      double dt = 2.0 * Math.PI / N;

      double x = 1.0;
      double v = 0.0;
      double t = 0.0;

      double xe,ve,xc,vc,xa,va;

      for(int i=0; i < N_CYCLES*N; i++)
      {
        t += dt;

        // Euler Method == Predictor
        xe = x + v * dt;
        ve = v - x * dt;

        // Corrector
        xc = x + 0.5 * (v + ve) * dt;
        vc = v - 0.5 * (x + xe) * dt;

        // Analytical values for k/m = 1.0;
        xa = Math.cos((i+1)*dt);
        va = - Math.sin((i+1)*dt);

        // Compare to analytical values
        if((i % N_PRINT) == 0)
        {
         double xdif = Math.abs(xc - xa);
         System.out.println("x error = "+xdif);
         double vdif = Math.abs(vc - va);
         System.out.println("v error = "+vdif);
        }

        // Use Corrected values for next point.
        x = xc;
        v = vc;
      }

    //-----------------------------------------------
  // and this line.
  }

  // Paint message in Applet window.
  public void paint(java.awt.Graphics g)
  { g.drawString("Spring_Applet1",10,20); }
}

Application version:
Spring_App1.java

The output of the program will show gradually increasing discrepancies of the numerical values from the analytical values as the cycles continue.

Exercise: Modify the Spring demo program to carry out many cycles, e.g. 20 or 100. Does the discrepancy with the analytical value become more and more significant?