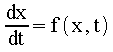Introduction
Essentials
Structure
Keywords
Primitive Types
Comments
Literals
Expressions
Operators
Statements
Casts & Mixing
Strings
Console Output 
   Demo
Exercises

    Supplements
Conditional: if-else
Repetitions
Flow Control
Java vs C/C++
JVM Instructions 1

The Euler method provides the simplest approach for solving ODEs and most of the more sophisticated techniques derive from it. In the Euler approach, the first order differential equation

can be approximated by making small increments in t and assuming that the slope, f(x,t), is nearly constant over those increments. So, beginning at point x₀, the next point x₁ becomes

for small dx, which relates to the increment in dt as

then

Repeating for the next point

This can be summarized in the finite difference equation:

The Euler method assumes that the slope f(x_n,t_n) evaluated at the point (x_n,t_n) remains approximately constant over the dt interval to x_(n+1).

See the demonstration of the Euler Method for the case of an object falling in a constant gravitational field.

Latest update: Dec.12.2003

            Tech
Arithmetic Ops
Math Class
More on Integers
FP : Overview
FP : Java  
  Demo 1
More Mix/Cast
  Demo 2
Exercises

           Physics
Differential Eq.
Euler Method
  Demo 1
Predictor-Corrector
  Demo 2
Exercises