
| Home : Map : Chapter 5 : Java : Tech : Physics : |
|
Interpolation Techniques
|
| JavaTech |
| Course Map |
| Chapter 5 |
|
File/Package/Import Demo 1 Demo 2 Access/Visibility final & Constants Static Import Jar Files Demo 3 Applet Directories 3rd Party Packages CLASSPATH javadoc CodingConventions Exercises |
|
Supplements
|
| About
JavaTech Codes List Exercises Feedback References Resources Tips Topic Index Course Guide What's New |
Suppose that you measured N values of a physical quantity y that depends on parameter x. You seek to find a function that will represent the data at the N points,
![]()
and will provide a good estimate for the physical quantity at a general value of x.
The most straight-forward technique is to interpolate between each pair of points with a straight line, as in :
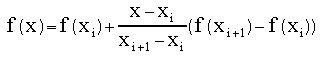
or
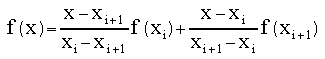
which is accurate to O(x2).
For sharp edged functions, this interpolation can actually provide a more accurate approximation than higher order approaches. However, if the function is smooth and curvy then higher order polynomial interpolations can provide a more accurate estimation.
For example, we could use three points to create a 2nd order polynomial:
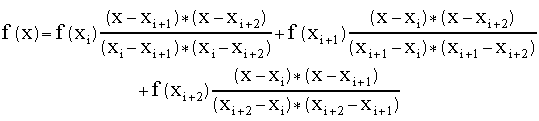
This is generalized with the Lagrange formula that provides an Nth order polynomial to fit through N points:
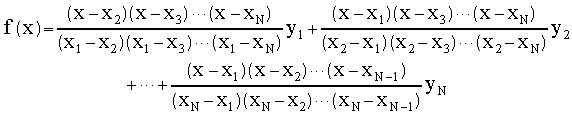
References & Web Resources
|
Tech |
|
Physics |