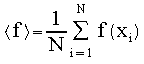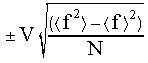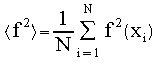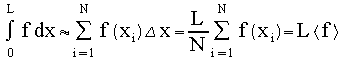|
The Monte Carlo (MC) approach to integration uses
random sampling to obtain a statistical estimate of the integral.
It provides a powerful approach when tackling integration of complicated
functions in multidimensional spaces.
The MC integral of function f over a volume V
goes as [Press]
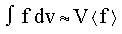
where
<f> equals the mean of the
function at N randomly sampled points:
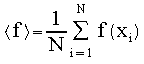
The standard deviation provides an error estimate:
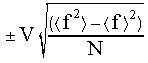
where
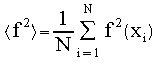
We can apply this to integration of a function of
a single variable as follows:
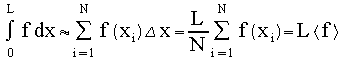
For the MC the mean <f>
comes from randomly selected xi
rather than a sequence. Nevertheless, for an increasing number of
random points the mean values should agree within a decreasingly
small error.
Another Monte Carlo approach to the same problem is
to view the plot of f(xi)vs
xi as a 2-D box of width L
and a height h
greater than or equal to the largest value of f(xi).
(See the demonstration program below.) A given number of points
are randomly sampled over the area. The total box area (L*h)
times the ratio of the number of points below the f(xi)
curve to the total number of points thrown provides an approximation
to the integrated area of the function.
We can relate this to the above calculation if we
let
f(x)
= frac(x)*h
where frac(x)is
the fraction of the box height that the function takes at point
x. Then the above
integral approximation goes as
L<f>
= L <frac> * h = V
* <frac>
where the average fractional value should in the limit
of increasing samples equal the fractional area calculated from
the scatter point distribution method.
The demonstration program below illustrates this type
of integration of a 1-D function. We use a subclass of PlotFormat
to display a function and the scatter of points. An interface called
Function
is used to provide a general type for creating different kinds of
functions.
MCPlotApplet.java
- integrates 1-D functions using a Monte
Carlo approach. The user generates different functions
via the buttons.
+ New classes
MCPanel.java
- subclass of PlotPanel that draws a function and the
scatter of points used for the MC integration. The function
plot is created with a Polygon object. By wrapping the
points around the boundary we can use the contains() function
in Polygon to obtain the number of points below the function
curve.
SinFunc.java
- function used to generated the curve to integrate. Implements
the Function interface.
Function.java
- interface to allow different types of functions to be
used for the MC demo.
+ Previous
classes:
Chapter
6:Tech: PlotPanel.java,
PlotFormat.java
|
|
import
javax.swing.*;
import java.awt.*;
import java.awt.event.*;
import java.util.*;
import java.io.*;
import java.net.*;
/**
* Plot a function and integrate it with the
Monte Carlo
* method.
*
* The applet uses the MCPanel subclass of PlotPanel
for the graphics
* output. Includes "Go","Clear",
and "Exit"
* buttons to initiate processing, clear the
text area, and exit
* when in standalone mode. A TextField displays
the integral
* value.
*
* The function comes from an implementation
of the Function
* interface.
*
* This program will run as an applet in a browser
or inside
* an application frame.
*
**/
public class MCPlotApplet extends JApplet
implements ActionListener
{
MCPanel fMcPanel;
// A text field for display of the integral
value.
JTextField fTextField;
// Flag for whether the applet is in a browser
// or running via the main () below.
boolean fInBrowser = true;
//Buttons
JButton fGoButton;
JButton fClearButton;
JButton fExitButton;
// Upper and lower values of the plot.
double fLoX=1.0;
double fHiX=10.0;
double fLoY=-1.0;
double fHiY=10.0;
// An implementation of the Function interface
provides
// the values of the given function.
Function fFunc;
// Settings for the function.
double fOffset = 2.0;
// Use default of 500 random points for the
MC integration.
int fNumPoints = 500;
/** Set up the interface. **/
public void init () {
JPanel panel = new JPanel (new BorderLayout
());
fFunc = new SinFunc ();
fFunc.setOffset (fOffset);
// an instance of MCPanel
fMcPanel = new MCPanel (fFunc, fHiY,
fHiX,
fLoY, fLoX);
panel.add (fMcPanel,"Center");
// Use a textfield for an input
parameter.
fTextField = new JTextField ("Integral
value", 15);
// Only used here for output
fTextField.setEditable (false);
// If return hit after entering
text, the
// actionPerformed will be invoked.
fTextField.addActionListener (this);
fGoButton = new JButton ("Go");
fGoButton.addActionListener (this);
fClearButton = new JButton ("Clear");
fClearButton.addActionListener (this);
fExitButton = new JButton ("Exit");
fExitButton.addActionListener (this);
JPanel control_panel = new JPanel
();
control_panel.add (fTextField);
control_panel.add (fGoButton);
control_panel.add (fClearButton);
control_panel.add (fExitButton);
panel.add (control_panel,"South");
// Add text area with scrolling
to the contentPane.
add (panel);
// The exit button only works in
the application
// so disable it so the user is
not confused.
if (fInBrowser) fExitButton.setEnabled
(false);
} // init
/** Use buttons to run the integrations. **/
public void actionPerformed (ActionEvent e)
{
Object source = e.getSource ();
if (source == fGoButton || source
== fTextField ) {
// In general it is
better to spin off
// extensive calculations
into a new thread
// rather than in an
event thread. However,
// we haven't reached
the thread chapter yet.
integrateFunction ();
}
else if (source == fClearButton)
{
fMcPanel.setDrawState
(MCPanel.DRAW_CLEAR);
fMcPanel.repaint ();
}
else if (!fInBrowser)
System.exit (0);
} // actionPerformed
/** Create a new function and use the MC method
to
* integrate it. Most of the work
is done in the
* the MCPanel class.
**/
void integrateFunction () {
fMcPanel.setDrawState (MCPanel.DRAW_POLY);
// Create a new function and plot
it.
// Modify the offset each time so
that
// the function is in the mid-range
section.
fOffset =
Math.random () * 0.8*
(fHiY - fLoY) + fLoY + 1.0 ;
fFunc.setOffset (fOffset);
fMcPanel.makeFunction ();
// Now create the scatter of random
points and
// calculate the integral the MC
way.
double integral = fMcPanel.makePoints
(fNumPoints);
String str =
PlotFormat.getFormatted
( integral, 1000.0 ,3);
fTextField.setText ("Integral =
" + str);
repaint ();
} // integrateFunction
public static void main (String[] args) {
int frame_width=450;
int frame_height=300;
// *** Modify applet subclass name
to that of the program
MCPlotApplet applet = new MCPlotApplet
();
applet.fInBrowser = false;
applet.init ();
// Following anonymous class used
to close window & exit program
JFrame f = new JFrame ("Demo");
f.setDefaultCloseOperation (JFrame.EXIT_ON_CLOSE);
// Add applet to the frame
f.getContentPane ().add ( applet);
f.setSize (new Dimension (frame_width,frame_height));
f.setVisible (true);
} // main
} // MCPlotApplet
|
|
/**
Use a sine function class implementing the Function interface.
*/
class SinFunc implements Function
{
double fOffset = 0.0;
public double value (double x) {
return Math.sin(x)+ offset;
}
public void setOffset(double o) {
offset = o;
}
} // SinFunc
/**
Interface to use for functions. */
public interface Function
{
// Return a double
value
public double value (double x);
public void setOffset (double o);
} // Function
|
|
import
java.awt.*;
import javax.swing.*;
/**
* Draws a 1-D function as a polygon
and the scatter of
* random points of the Monte Carlo
using PlotPanel superclass.
* Does the calculation of the integral using
the Polygon's
* contains () method to find the
number of points below
* the function area.
**/
public class MCPanel extends PlotPanel
{
String fTitle = "Monte Carlo Plot";
String fXLabel= "Y vs X";
Polygon fPoly;
// Constants to indicate type of drawing
final static int DRAW_POLY = 1;
final static int DRAW_PTS = 2;
final static int DRAW_CLEAR= 3;
int fDrawState = DRAW_CLEAR;
int [][] fRanPoints;
int fNumRanPoints = 0;
// Convert from the screen coordinates to the
// scale of the variables.
double fYConvert = 0.0;
double fXConvert = 0.0;
// Symbol types for plotting the function
final static int SOLID = 0;
// Student can add other line types such as
// dotted and dashed
int fLineType = 0;
// These numbers determine the axes ranges.
double fYDataMax = 1.0;
double fXDataMax = 1.0;
double fYDataMin = 0.0;
double fXDataMin = 0.0;
// Default numbers to use for plotting axes
scale values
double [] fXScaleValue;
double [] fYScaleValue;
int fNumYScaleValues = 5;
int fNumXScaleValues = 5;
// Instance of the interface Function
Function fFunc;
/**
* Passes an instance of Function
and the limits
* to the plot.
**/
public MCPanel (Function f,
double yDataMax, double xDataMax,
double yDataMin, double xDataMin){
fFunc = f;
fYDataMax = yDataMax;
fXDataMax = xDataMax;
fYDataMin = yDataMin;
fXDataMin = xDataMin;
getScaling ();
} // ctor
/** Reset the function and the limits. **/
public void setFunction (Function f,
double yDataMax, double xDataMax,
double yDataMin, double xDataMin) {
fFunc = f;
fYDataMax = yDataMax;
fXDataMax = xDataMax;
fYDataMin = yDataMin;
fXDataMin = xDataMin;
getScaling ();
repaint ();
} // setFunction
/**
* Get the values for
the scaling numbers on
* the plot axes.
**/
void getScaling () {
fYScaleValue = new double[fNumYScaleValues];
// Use lowest value of 0;
fYScaleValue[0] = fYDataMin;
fYScaleValue[fNumYScaleValues-1]
= fYDataMax;
// Then calculate the difference
between the values
double range = fYScaleValue[fNumYScaleValues-1]
-
fYScaleValue[0];
double del = range/ (fNumYScaleValues-1);
// Now set the intermediate scale
values.
for (int i=1; i < (fNumYScaleValues-1);
i++) {
fYScaleValue[i]
= i*del + fYScaleValue[0];
}
fXScaleValue = new double[fNumXScaleValues];
// First get the low
and high values;
fXScaleValue[0] = fXDataMin;
fXScaleValue[fNumXScaleValues-1]
= fXDataMax;
// Then calculate the difference
between the values
range = fXScaleValue[fNumXScaleValues-1]
- fXScaleValue[0];
del = range/ (fNumXScaleValues-1);
// Now set the intermediate scale
values.
for (int i=1; i < (fNumXScaleValues-1);
i++) {
fXScaleValue[i]
= i*del + fXScaleValue[0];
}
} // getScaling
/** Set switch for draw state. **/
public void setDrawState (int state) {
fDrawState = state;
}
/** Find the points used to plot
the function. We wrap the
* points back around
the boundary so that we can use the
* contains () method
in the Polygon class to find the
* number of points below
the function curve. (See the makePoints
* method.)
**/
void makeFunction () {
// Need conversion factor from data
scale to pixel scale
fYConvert = fFrameHeight/ (fYDataMax
- fYDataMin);
fXConvert = fFrameWidth / (fXDataMax
- fXDataMin);
// Want to draw the plot for the
width of the
// frame plus points to wrap around
the lower boundary
// and back to the first point.
int numPoints = fFrameWidth + 4;
int [] x = new int[numPoints];
int [] y = new int[numPoints];
int maxY = fFrameY + fFrameHeight;
// Distance between each pixel
double dx = (fXDataMax
- fXDataMin)/fFrameWidth;
// Get the function values to create
a polygon
for (int i=0; i < numPoints-3; i++)
{
double xFunc = fXConvert*
(dx * i);
x[i] = (int)xFunc
+ fFrameX;
double yFunc = fYConvert
* fFunc.value (dx * i + fXDataMin);
y[i] = maxY - (int)yFunc;
if (y[i] < fFrameY)
y[i] = fFrameY;
else
if (y[i] > maxY) y[i]
= maxY;
}
// Bottom right corner
x[numPoints-3] = fFrameX + fFrameWidth;
y[numPoints-3] = maxY;
// Bottom left corner
x[numPoints-2] = fFrameX ;
y[numPoints-2] = maxY;
// Back to first point.
x[numPoints-1] = x[0] ;
y[numPoints-1] = y[0];
// Create a polygon object from
these point arrays
fPoly = new Polygon (x,y,numPoints);
} // makeFunction
/** Create the distribution of random
points
* and calculate the MC
integral from the
* fraction of the points
under the function
* curve. Use the Polygon class's
contains () method.
**/
double makePoints (int nPoints) {
fNumRanPoints = nPoints;
// Could thrown an exception here
but instead
// return negative value as a flag.
if (fNumRanPoints <= 0 ) return
-1.0 ;
fRanPoints = new int[fNumRanPoints][2];
int numInside = 0;
setDrawState (MCPanel.DRAW_PTS);
// Make a scatter of points for
the MC integration.
for (int i=0; i< fNumRanPoints;
i++) {
fRanPoints[i][0]= (int)
(Math.random () * fFrameWidth) + fFrameX;
fRanPoints[i][1]= fFrameY+fFrameHeight
-
(int)
(Math.random () * fFrameHeight) ;
// Take advantage of
the contains () method in Polygon
// to get the number
of points below the function curve.
if (fPoly.contains (
fRanPoints[i][0], fRanPoints[i][1]) )
numInside++;
}
double fraction = (double)numInside/
(double)fNumRanPoints;
double integral = fraction * (fYDataMax
- fYDataMin)* (fXDataMax - fXDataMin);
repaint ();
return integral;
} // makePoints
/**
* Draw the function and the scale
values. When flag set,
* also draw the random
points.
**/
void paintContents (Graphics g) {
// No contents or scale values draw
when clear flag set.
if (fDrawState == DRAW_CLEAR) return;
// Then pass the polygon object
for drawing
g.drawPolygon (fPoly);
// Draw the numbers along the axes
drawAxesNumbers (g, fXScaleValue,
fYScaleValue);
if (fDrawState == DRAW_PTS) {
for (int i=0; i < fNumRanPoints;
i++) {
g.fillOval
(fRanPoints[i][0],fRanPoints[i][1],2,2);
}
}
} // paintContents
/** Methods overriding those in PlotPanel. **/
String getTitle ()
{ return fTitle;}
String getXLabel ()
{ return fXLabel;}
/** Additional methods for setting the title
and label. **/
void setTitle (String title)
{ fTitle = title;}
/** Set label along horizontal axis. **/
void setXLabel (String fXLabel)
{ this.fXLabel = fXLabel;}
/** Set the type of line. **/
void setLineType (int type) {
if (type < 0 || type > 0) return;
fLineType = type;
}
} // MCPanel
|
Similar approaches can work for multi-dimensional
integrations. Note that the bounding volume need not be "square"
as in the above box example but needs only to exceed the function
at all points. In fact, it is best if the bounding volume just slightly
exceeds the function since only points inside the function provide
"information content" and serve to reduce the error estimate.
Monte Carlo integrations provide powerful tools for
many physics analysis situations, especially "event" type
phenomena such as in particle scattering studies. We will discuss
in Chapter 11 : Physics how
Monte Carlo integration with simulations of the particle scattering
and the detectors provide the cross sections.
References
& Web Resources
Latest update: Feb.16.2003
|